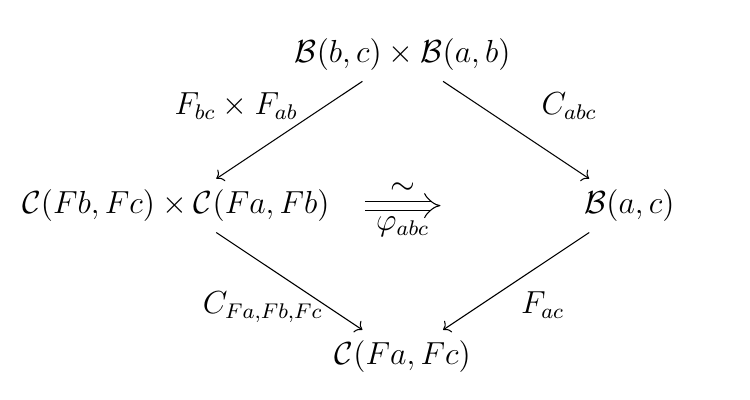
任意の $a, b, c \in \mathrm{Ob}(\mathcal{B})$ に対し次のような自然同型 $\varphi_{abc}$ が与えられている.
函手(functor)の双圏版が擬函手(pseudofunctor)である. なお, 「擬函手」という訳は本稿独自であり, 推奨しない. 以降は「pseudofunctor」で統一する.
$\mathcal{B}, \mathcal{C}$ を bicategory とするとき, $F \colon \mathcal{B} \to \mathcal{C}$ が pseudofunctor(もしくは weak 2-functor)であるとは, 以下を満たすことを言う.
任意の $a, b, c \in \mathrm{Ob}(\mathcal{B})$ に対し次のような自然同型 $\varphi_{abc}$ が与えられている.
