圏の積と双函手
圏の積
全ての圏からなる圏 $\mathbf{CAT}$ においては積が定義できる. なお, 積の定義については参考文献等を参照されたい.
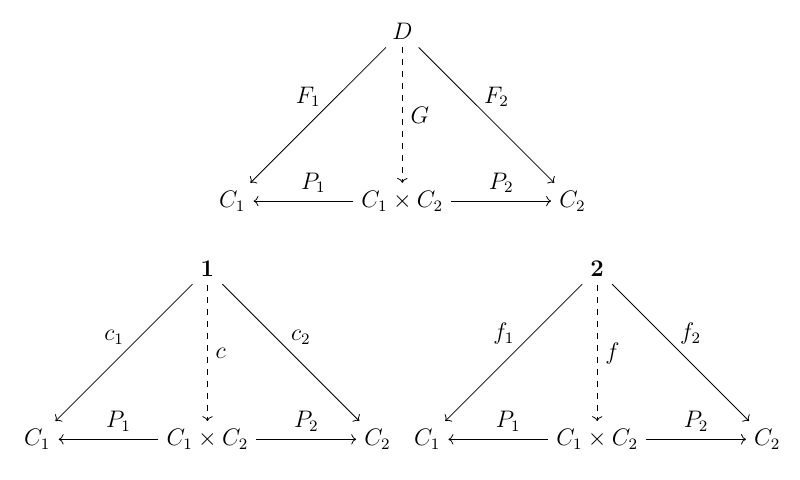
上図から $C_1 \times C_2$ の
- 対象は対 $(c_1, c_2)\quad (c_1 \in \mathcal{O}(C_1), c_2 \in \mathcal{O}(C_2))$,
- 射は対 $(f_1, f_2)\quad (f_1 \in \mathcal{M}(C_1), f_2 \in \mathcal{M}(C_2))$,
-
$(f_1, f_2)$ と $(g_1, g_2)$ の合成は $f_1 \circ g_1$ と $f_2 \circ g_2$ がともに定義されるときに限り定義され
$$(f_1, f_2) \circ (g_1, g_2) = (f_1 \circ g_1, f_2 \circ g_2)$$
と考えることができる.
双函手
定義
函手 $F \colon C \times D \to B$ はしばしば双函手と呼ばれる. これには以下の性質がある.
-
各 $c \in \mathcal{O}(C)$ に対して $F^c(d) = F(c, d), F^c(g) = F(1_c, g)$ とおくと,
$F^c : D \to B$ は函手.
-
各 $d \in \mathcal{O}(D)$ に対して $F_d(c) = F(c, d), F_d(f) = F(f, 1_d)$ とおくと,
$F_d : C \to B$ は函手.
-
$F^c(d) = F_d(c)$, かつ $f \colon c \to c', g : d \to d'$ について
$F^{c'}(g) \circ F_d(f) = F_{d'}(f) \circ F^c(g)$.
逆に, 上記の性質を満たす函手の族 $\{ F^c \colon D \to B \}_{c \in \mathcal{O}(C)}, \
\{ F_d \colon C \to B \}_{d \in \mathcal{O}(D)}$ があれば, ただ一つの双函手
$F \colon C \times D \to B$ が定義できる.
双函手の例
-
$C$ が局所小圏のときの $\hom$ 函手 $\hom(-, -) \colon C^\mathrm{op} \times C \to \mathbf{Set}$.
-
$C, C', C''$ を圏とするとき $[C', C''] \times [C, C'] \to [C, C'']$ を
$(\alpha', \alpha) \mapsto \alpha' \star \alpha$ で定めると双函手になる.
双函手間の自然変換
$F, G \colon C \times D \to B$ を双函手とするとき, 射の族
$\{\alpha(c, d) \colon F(c, d) \to G(c, d)\}_{(c, d) \in \mathcal{O}(C \times D)}$ が自然変換
$F \stackrel{\bullet}{\to} G$ であることは
-
各 $c \in \mathcal{O}(C)$ に対する
$\{\alpha(c, d) \colon F^c(d) \to G^c(d)\}_{d \in \mathcal{O}(D)}$ が自然変換
$F^c \stackrel{\bullet}{\to} G^c$ かつ
-
各 $d \in \mathcal{O}(D)$ に対する
$\{\alpha(c, d) \colon F_d(c) \to G_d(c)\}_{c \in \mathcal{O}(C)}$ が自然変換
$F_d \stackrel{\bullet}{\to} G_d$
と同値である.
戻る

