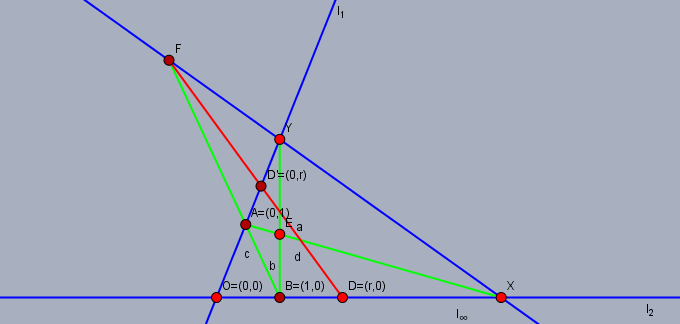
どの三点も同一直線上にない四点 $o, e, x, y$ を取り, $l_1 := o\vee y, l_2 := o\vee x, l_{\infty} := x\vee y$ とおく.
少なくとも二つの元 $0, 1(\ne 0)$ を含む集合 $R$ ($R$ の濃度は $l_1\setminus\{y\}$ の濃度と等しいものとする)を用意する. また $$a := (x\vee e)\cap l_1, b := (y\vee e)\cap l_2, f := (a\vee b)\cap l_{\infty}$$ とする.
全単射 $$\varphi : R\to l_1\setminus\{y\}$$ を $\varphi(0) = o, \varphi(1) = a$ となるように取る. $\varphi(r) = c$ のとき, $c := (0, r)$ と表記する. これにより $o = (0, 0), a = (0, 1)$ となる.
続いて $d\in l_2\setminus\{x\}$ に対し $d' := (f\vee d)\cap l_1$ とし, $d' = (0, r)$ であるとき $d := (r, 0)$ と表記する. これにより $b = (1, 0)$ となる.

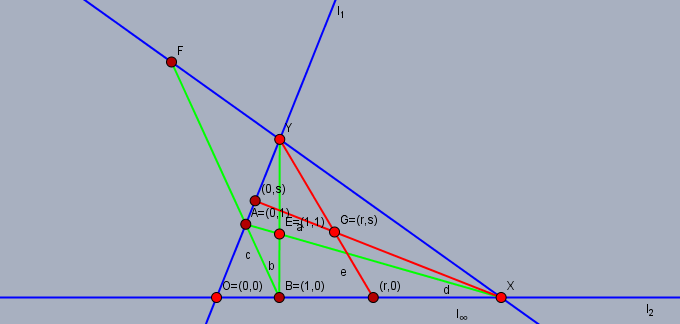
$l_{\infty}$ 上にない点 $g$ に対しては $(g\vee x)\cap l_1 = (0, s)$ かつ $(g\vee y)\cap l_2 = (r, 0)$ のとき $g := (r, s)$ と表記する. これにより $e = (1, 1)$ となる.
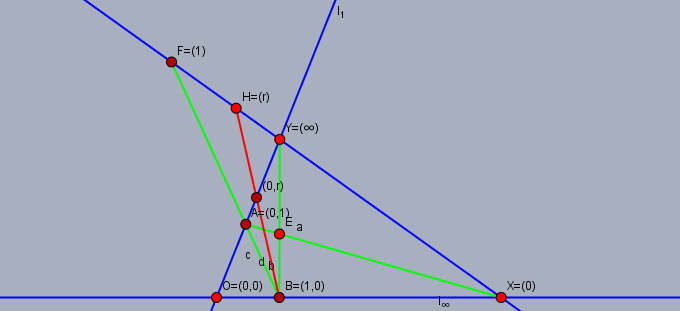
$l_{\infty}\setminus\{y\}$ の各点 $h$ に対しては $(h\vee b)\cap l_1 = (0, r)$ のとき $h := (r)$ と表記する. これにより $x = (0), f = (1)$ となる.
最後に $y := (\infty) (\infty\notin R)$ とする. これですべての点に対して座標が割り当てられた.
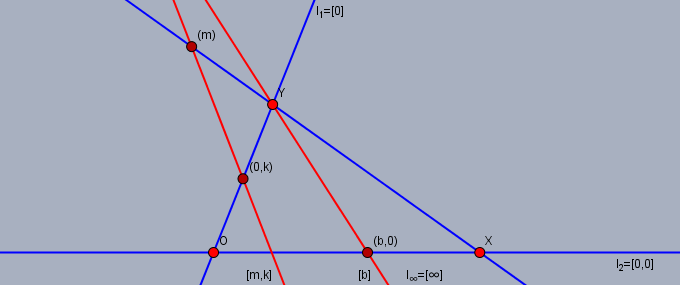
$y$ を通らない直線 $l$ については $l\cap l_{\infty} = (m)$ かつ $l\cap l_1 = (0, k)$ のとき $l := [m, k]$ と表記する. これにより $l_2 = [0, 0]$ となる.
$y$ を通る直線 $g(\ne l_{\infty})$ については $g\cap l_2 = (b, 0)$ のとき $g := [b]$ と表記する. これにより $l_1 = [0]$ となる.
最後に $l_{\infty} := [\infty]$ とする.