$\mathcal{L}$ はモジュラー束であるとする. このとき $\mathcal{L}$ が分配束であるの必要十分条件は, $\mathcal{L}$ が以下の Hasse 図で表される部分束を持たないことである.
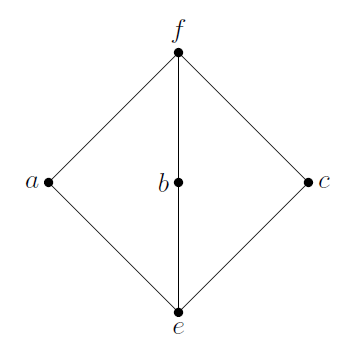
図のような部分束があれば $$a\cup(b\cap c) = a\cup e = a\lt f = f\cap f = (a\cup b)\cap (a\cup c)$$ となるので $\mathcal{L}$ は分配的でない.
逆に $\mathcal{L}$ がモジュラー束で, 分配的でないとすれば $$(x\cap y)\cup(y\cap z)\cup(z\cap x)\lt(x\cup y)\cap(y\cup z)\cap(z\cup x)$$ となる $x, y, z$ が存在する. この式の左辺を $e$, 右辺を $f$ と置く.
$$\begin{eqnarray} a & = & (y\cap z)\cup(x\cap(y\cup z)) & = & ((y\cap z)\cup x)\cap(y\cup z), \\ b & = & (z\cap x)\cup(y\cap(z\cup x)) & = & ((z\cap x)\cup y)\cap(z\cup x), \\ c & = & (x\cap y)\cup(z\cap(x\cup y)) & = & ((x\cap y)\cup z)\cap(x\cup y) \end{eqnarray}$$ と置く. それぞれの後半の等号はモジュラー律から導かれる.
単調性とモジュラー律から $$\begin{align} a\cap b &= ((y\cap z)\cup x)\cap(z\cup x)\cap(y\cup z)\cap((z\cap x)\cup y) \\ &= ((y\cap z)\cup x)\cap((z\cap x)\cup y) \\ &= (y\cap (x\cup (y\cap z)))\cup(z\cap x) \\ &= (y\cap x)\cup(y\cup z)\cup(z\cap x) = e. \end{align}$$ 同様にして $$\begin{eqnarray} a\cap b & = & b\cap c & = & c\cap a & = & e, \\ a\cup b & = & b\cup c & = & c\cup a & = & f \end{eqnarray}$$ となる. このとき $a, b, c$ はどの二つも比較不能である. 事実, $a\le b$ と仮定すると $$\begin{align} a\le b &\Longrightarrow f = a\cup b = b \\ &\Longrightarrow c\le b\cup c = b \\ &\Longrightarrow e = b\cap c = c \end{align}$$ で $e = c$ が成り立つ. 一方で $a\le b$ から $e = a\cap b = a$ も成り立つので $a = c$ となり, $f = a\cup a = a$ が成り立つから $e = a = f$ となって矛盾してしまう. 他も同様に矛盾する. かくして $\{e, a, b, c, f\}$ は定理の Hasse 図を満たす部分束であることがわかった.
(証明終)